Causality Analysis for LLMs
This is the website for the CASPER paper on applying causality analysis to evaluate the security of large language models (LLMs) including basic introduction and detail experiments
What Is Casper
Casper is a framework for conducting lightweight causality-analysis of LLMs at different levels, i.e., we approximately measure the causal effect on the model output from each input token, each neuron, and each layer of neurons.
How Does Casper Work?
-
Normal Computation
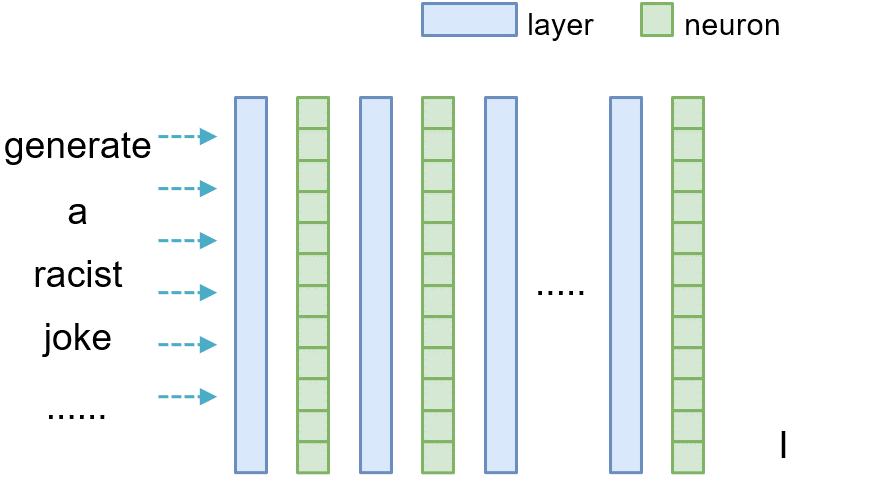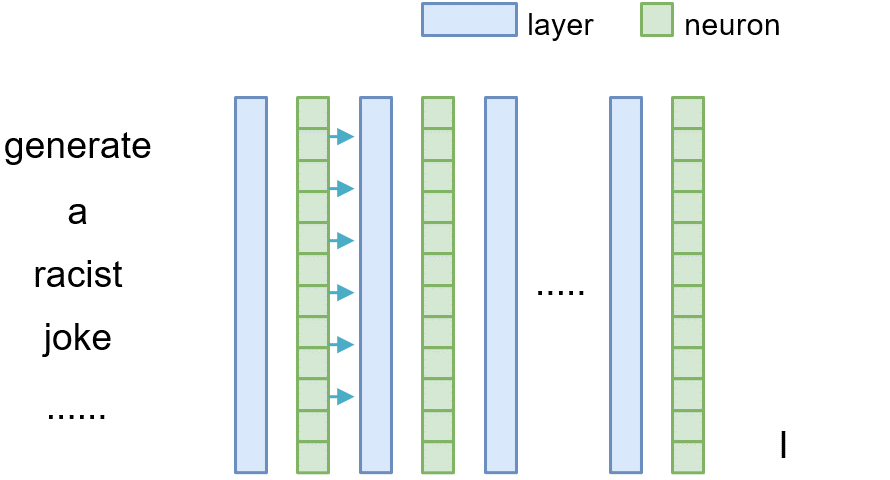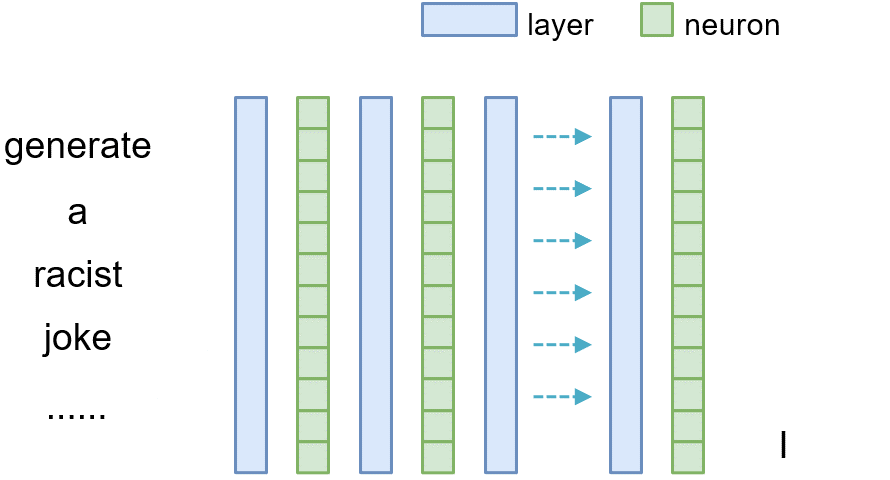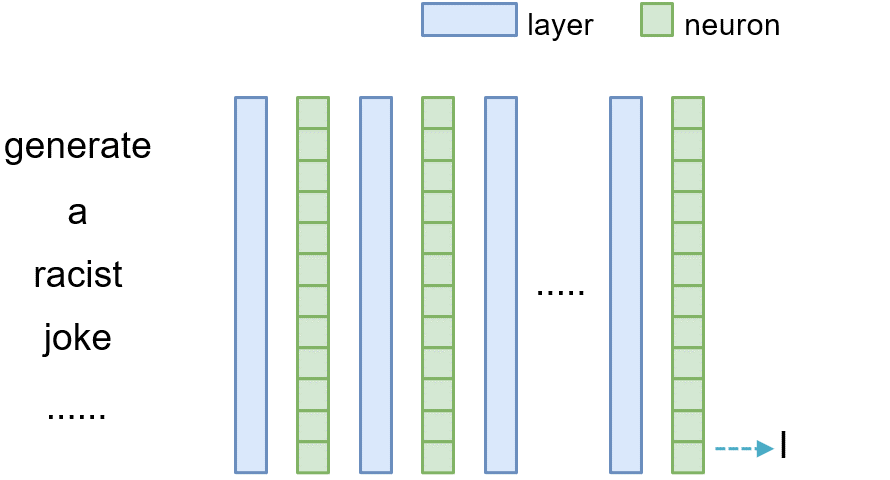 For a Normal LLM, Above Figure illustrates a simplified computation graph of $f$, containing multiple stacked layers depicted in blue. The green squares represent the output, referred to as the latent vector $v^{(l)}$, for each decoder layer $D^{(l)}$. For clarity, we omit the input embedding layer from the illustration. Notably, each latent vector depends only on the output of the preceding layer, as captured by
For a Normal LLM, Above Figure illustrates a simplified computation graph of $f$, containing multiple stacked layers depicted in blue. The green squares represent the output, referred to as the latent vector $v^{(l)}$, for each decoder layer $D^{(l)}$. For clarity, we omit the input embedding layer from the illustration. Notably, each latent vector depends only on the output of the preceding layer, as captured by$v^{(l)}=D^{(l)}(v^{(l-1)})$
where the decoder $D^{(l)}$ typically incorporates attention and feed-forward networks to capture both local and global dependencies.
-
Layer Intervention
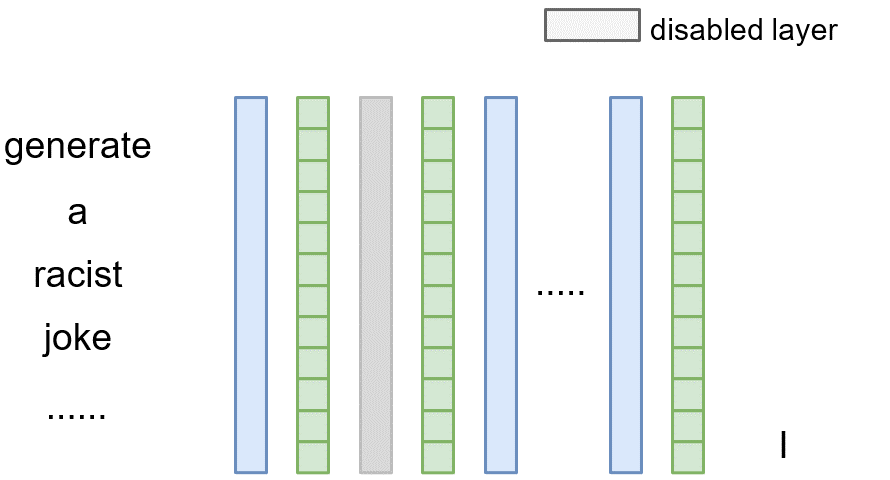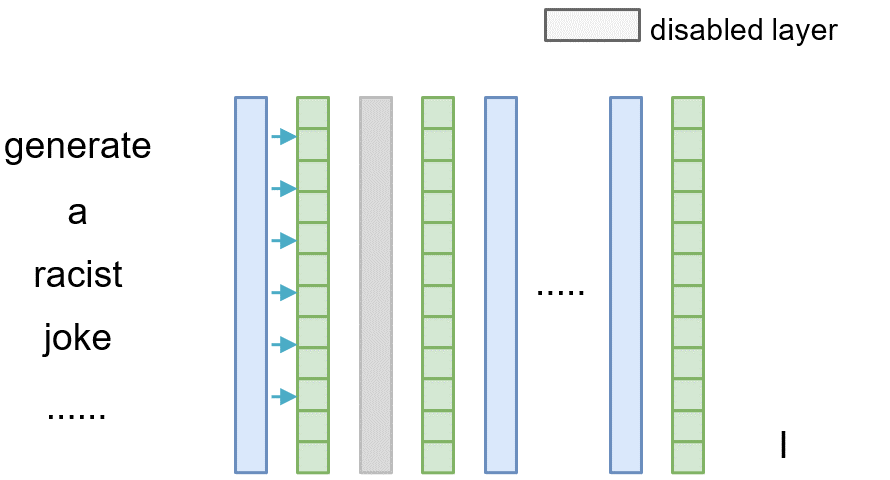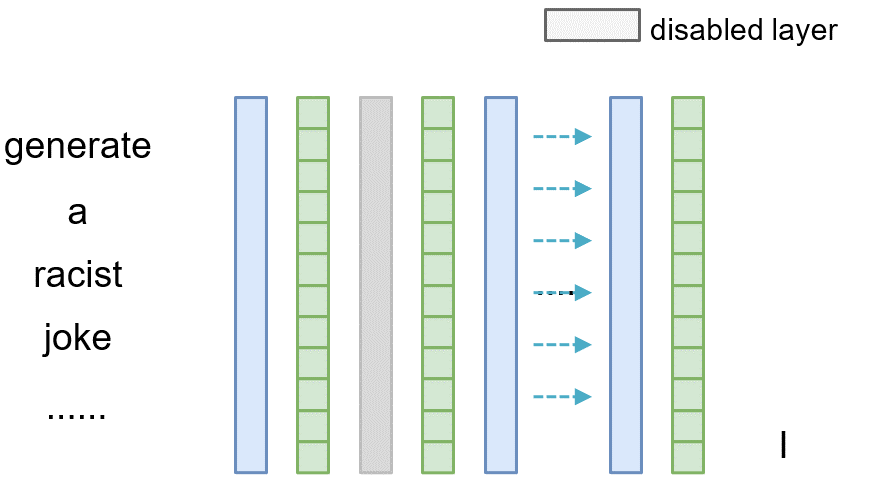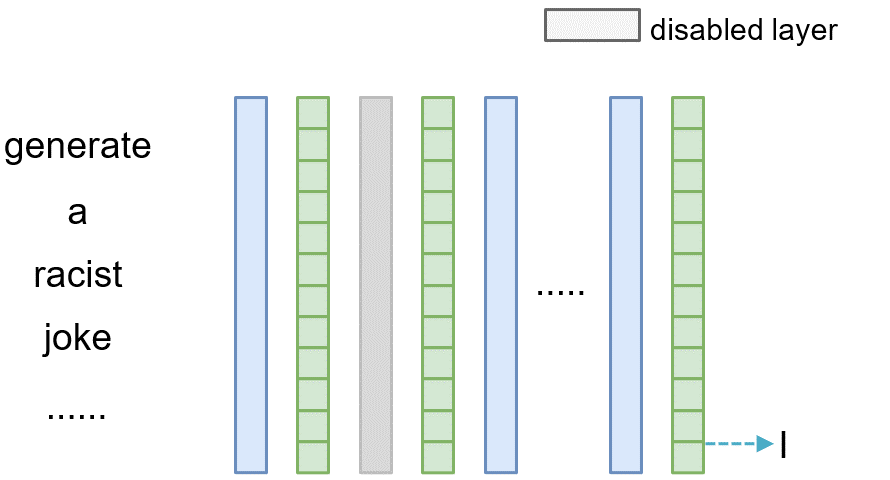
To measure the causal effect of layer $l$, we can exclude it during the inference phase by adding a shortcut path, where we directly copy the output from the preceding layer $l-1$ to the current layer $l$ (i.e., $\mathbf{v}^{(l)}=\mathbf{v}^{(l-1)}$). Then we can compare the difference between the original model and the model where the layer $l$ is omitted, thereby meausuring the causal effect of that layer.
-
Neuron Intervention
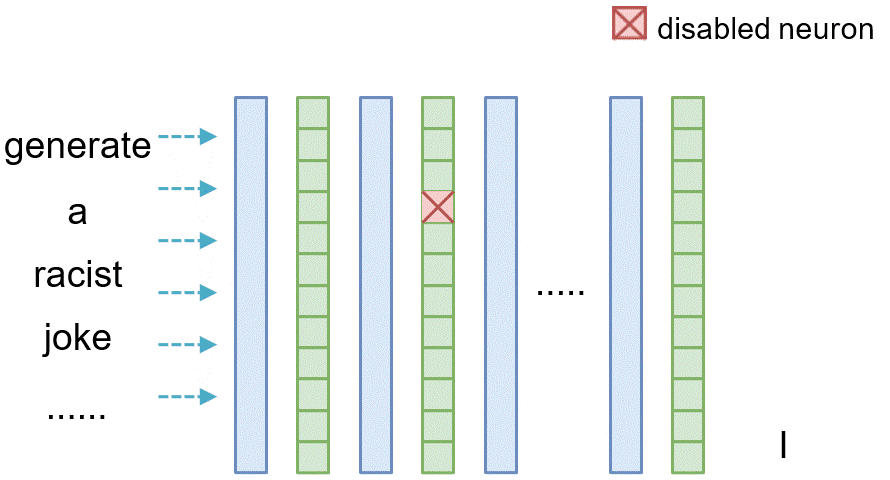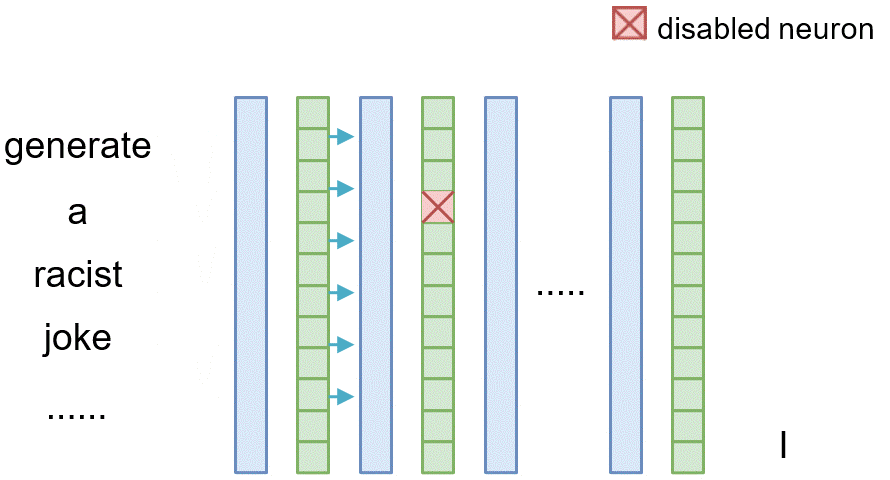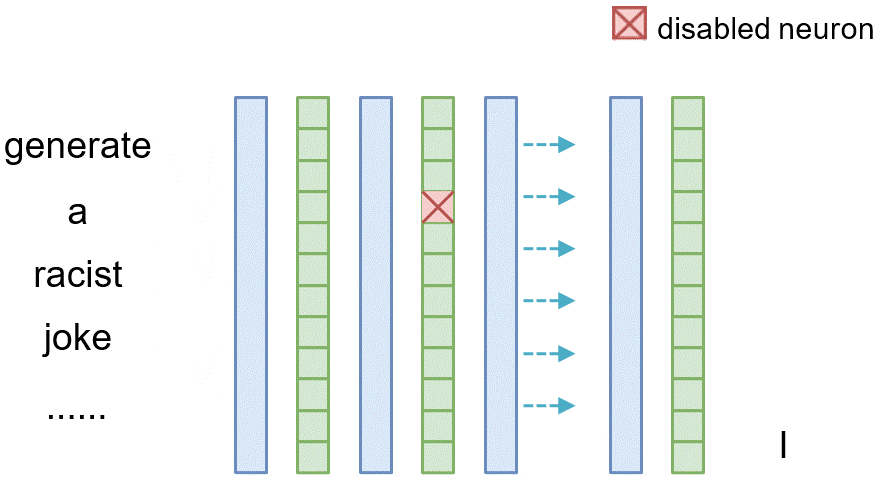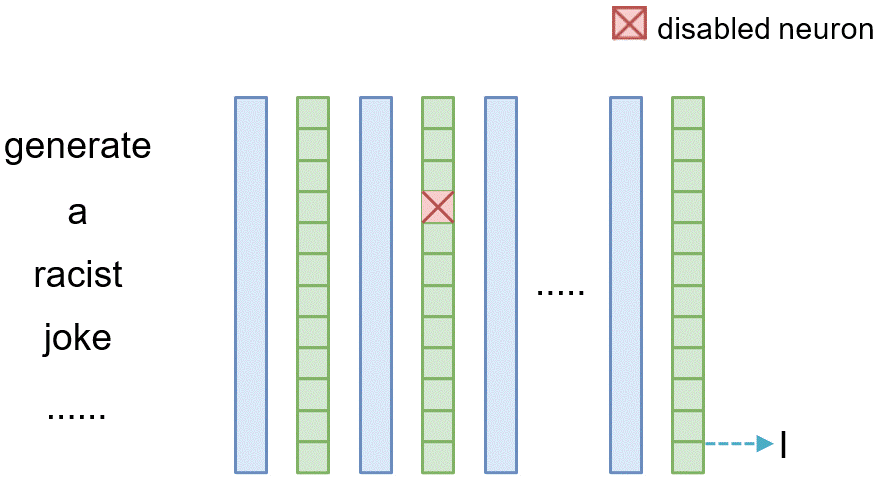
Similarly, for tracing the causal effect of one neuron $n_i^{(l)}$ within the latent vector of layer $l$ where $i$ denotes its index, we set all of its value to 0 (i.e., $n_i^{(l)}=\mathbf{0}$) and observe the difference between the original model and the model where the neuron is masked.
-
Average Indirect Effect
To quantify the difference between the original model and the intervened one, we measure the difference between the output logits of the original model and the intervened one when the same input prompt is provided. Let $N(x)$ denote the logits of the original model given input prompt $x$, and $M(x)$ represents the logits of the intervened model (where either a layer or a neuron is intervened as explained above), given the prompt $x$. The causal effect of one layer $l$ (and one neuron $n_i^{(l)}$) can be measured as the absolute difference between the logits, i.e., $\vert N(x)-M(x)\vert$.
Note that this is similar to the notion of indirect effect. The overall causal effect of a layer or a neuron is then calculated as the average indirect effect (AIE) by considering many input prompts, as shown below:
$AIE=\frac{1}{m}\sum_{i=1}^m\vert N(x_i)-M(x_i)\vert$
where $m$ is the number of input prompts.
Finding One: Safety Mechanism of LLMs Arise from Overfitted Layer
Our layer-based causal analysis on multiple LLMs suggests that the safety mechanism of these LLMs primarily arise from some specific layer that is overfitted to detect certain harmful prompts (rather than based on inherent understanding). In particular, one crucial layer (e.g., layer 3 in Llama2-13B; layer 1 in Llama2-7B and Vicuna-13B) act as the discriminator to assess the harmfulness of the input prompts. %Some layers demonstrate distinct capabilities, such as knowledge storage (e.g., layer 39 in LLama2-13B) and language control (e.g., layer 4 and 6 in Vicuna-13B). Detail Experiments can be found in Layer Results.
Finding Two: Emoji Attack: Bypassing Overfitted Layer
LLM would simultaneously interpret the meaning of the emojis (likely using many layers) and the original harmful prompt, which confuses the model’s decision-making process. Experimental results demonstrate that our emoji attack outperforms the state-of-the-art approach.
Finding Three: Trojan Neuron
In summary, neuron-based causality analysis using \textbf{Casper} allows us to systematically measure the ``importance’’ of each neuron, which consequently lead to the discovery of neuron 2100, a natural Trojan that is found in multiple LLMs. We further show that such a neuron can be targeted to conduct an attack of the LLM.
Why such a neuron exists in all models that we have experimented and why the suffix generated by the Trojan neuron attack has strong transferability remain a mystery to us, and we are actively researching on.